Semejanza

3. Centro de semejanza a partir de un punto exterior

Trazado de un triángulo semejante a partir de un punto exterior con una razón de semejanza de r=5/3.

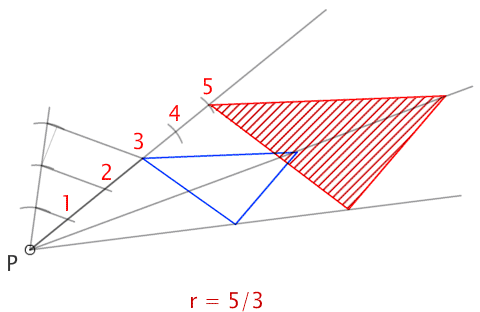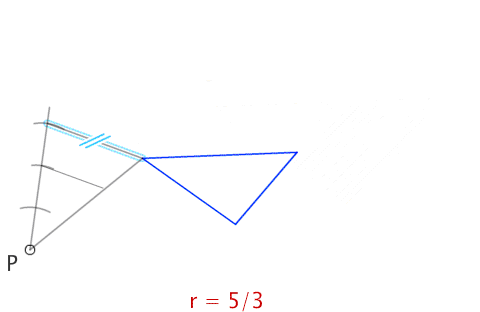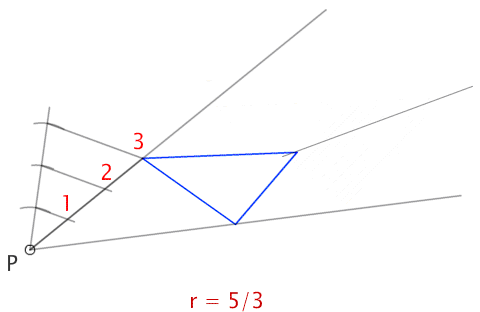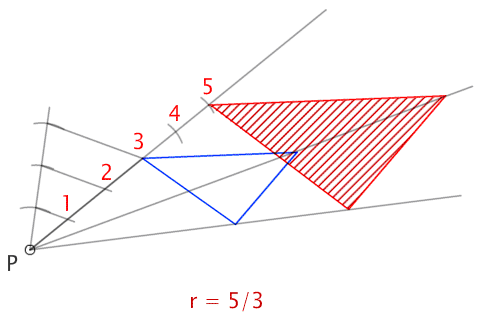
4. Centro de semejanza a partir de un vértice del polígono

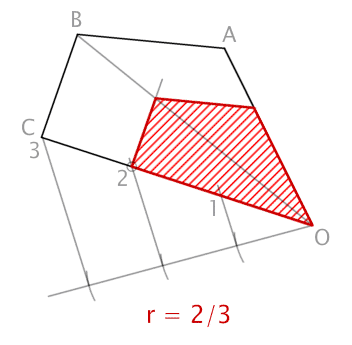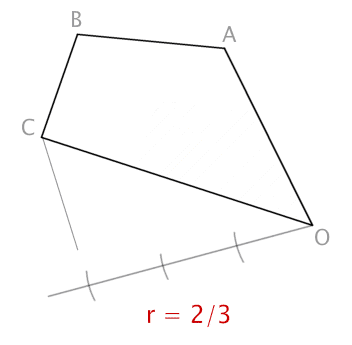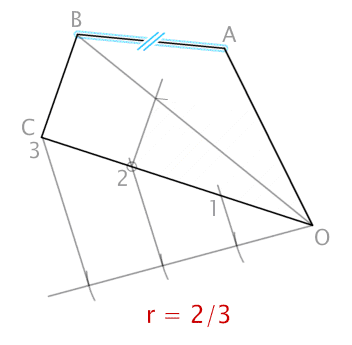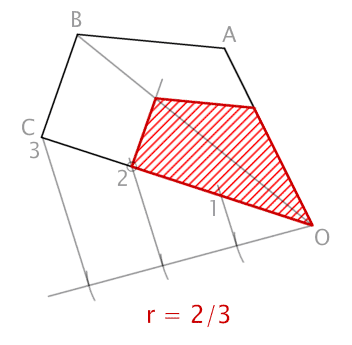
Trazado de un polígono irregular semejante a partir de un vértice del polígono con una razón de semejanza r=2/3.

 
 Homotecia conceptos básicos

Aquí vemos un caso de HOMOTECIA NEGATIVA o INVERSA. El centro de homotecia O, quedará entre las dos figuras: la dada y la resultante. Dado que K=-2 la figura resultante tendrá el doble de tamaño que la original y sentido contrario. O estará entre ambas figuras.

OA´=2OA´

Enlace a imagen de Homotecia directa 

e inversa
Aquí tenéis otro caso de homotecia negativa o inversa, en la que además el centro de homotecia es un vértice del polígono.

 

Transformaciones geométricas isomórficas

En geometría las transformaciones geométricas isomórficas son aquellas que solo conservan la forma; es decir, en ellas los ángulos de la figura original y de la transformada son iguales y las longitudes proporcionales.

1. Clasificación

1.1 Semejanza

Dos figuras son semejantes cuando tienen la misma forma (el mismo número de lados y ángulos iguales) y distinto tamaño (sus dimensiones son distintas).

Los diversos elementos que en las figuras semejantes se corresponden son proporcionales entre sí, existiendo igualdad entre sus ángulos.

Esta correspondencia se denomina Razón de Semejanza (K) y es la relación de proporcionalidad constante que existe entre los elementos de las dos figuras semejantes.

2. Homotecia

La Homotecia es una transformación geométrica, una correspondencia entre dos figuras en la que se cumple que las parejas de puntos homotéticos están alineados con el centro de homotecia O y los segmentos homotéticos son paralelos.

• Homotecia Directa: Cuando los dos puntos homotéticos se encuentran al mismo lado respecto al centro, la homotecia es directa. Las figuras homotéticas directas son semejantes y nunca son equivalentes.

• Homotecia Inversa: Cuando los puntos homotéticos se encuentran alineados con el centro pero en extremos opuestos de las radiaciones, la homotecia es inversa. En este caso la figura no es semejante, es el producto de dos simetrías axiales cuyos ejes, uno vertical y otro horizontal, pasan por el centro de homotecia.

• Factor de proporcionalidad en la Homotecia: El factor de proporcionalidad o razón de semejanza entre figuras homotéticas directas es siempre positiva. Las figuras homotéticas inversas responden a un factor de proporcionalidad negativo, son equivalentes si el factor de proporcionalidad es-1.